Una ya larga tradición de fórmulas y modelos permite predecir la lecturabilidad y mejorar la comprensión de textos en español. Ahora pueden aplicarse en tiempo real a los medios de comunicación escritos y orales, incrementando su eficacia.
1. ¿ECUACIONES EN LA REDACCIÓN?
No parece que las paredes de las redacciones sean el lugar más propicio para fijar ecuaciones. Otra cosa es que en las paredes aparezcan grabadas las ideas que expresan las ecuaciones, pero de un modo más directo. No en balde uno de los atributos del periodista es hacer inteligible lo arduo.
En ninguna redacción de periódico creo que aparezca en cuadro, hoja de post-it, cartel o pegatina la fórmula que enuncia:
![]()
Pero estoy seguro que ningún periodista ignora que la noticia es que un hombre muerda a un perro, no a la inversa.
Tampoco imagino que sea elemento de poster, pasquín o motivo de marco para ser exhibida en el entorno profesional de los periodistas una fórmula que diga que:
Lect.= 9,5 – 9,7 (1/p) – ,35 (p/f)
Pero cabe pensar que en el trabajo diario de un periodista será frecuente recordar el donaire de aquel profesor de retórica, por nombre Juan de Mairena, al que diera vida don Antonio Machado:
«Señor Pérez, salga usted a la pizarra y escriba:
los eventos consuetudinarios que acontecen en la rúa.
El alumno escribe lo que se le dicta.
– Vaya usted poniendo eso en lenguaje poético.
El alumno, después de meditar, escribe:
Lo que pasa en la calle
Mairena: No está mal»
Las diferencias entre la frase dictada por Mairena y la versión del señor Pérez son las que aparecen expresadas en la formula de lecturabilidad de Gutiérrez de Polini (1972), y que pone de manifiesto que palabras más largas y frases más largas dificultan la lectura. La valoración de la lecturabilidad,de la facilidad o dificultad de un texto escrito para ser comprendido por un lector, se calcula, en la fórmula transcrita por medio de esos dos parámetros. En dicha fórmula, ( l / p ) es el promedio de letras por palabra y ( p / f ) es el promedio de palabras por frase. Es decir: se predice, a partir de elementos constatables directamente en el texto, el nivel de dificultad o facilidad de un texto para ser entendido.
Voy a presentar aquí una serie de fórmulas de predicción de lecturabilidad aplicables al castellano, y en concreto a tres grupos de lectores: un grupo de buenos lectores, otro de lectores medios, definidos por el nivel de formación académica que poseían, y un grupo general, constituido por la integración de los dos grupos anteriores.
Se pretende que estas fórmulas sean de aplicación al mundo de la prensa escrita.
Nuevamente de actualidad
Las fórmulas de predicción de lecturabilidad constituyen uno de los medios clásicos de análisis de la eficiencia comunicativa del lenguaje verbal escrito.
En algún momento han parecido perder fuerza estos instrumentos de análisis. Sin embargo hay, en el momento presente, dos líneas al menos que contribuyen a poner de nuevo sobre el tapete el tema de la lecturabilidad. Una tiene un componente teórico a la base. La otra es una constatación empírica. Y sobre ambas se impone la conveniencia de tener una indicación aproximativa inicial que, a través de los textos procesados por ordenador, pueden obtenerse automáticamente y casi en tiempo real.
Comencemos con el argumento teórico. Es necesario entender la lectura como un proceso interactivo. La interacción entre el emisor de un mensaje y el receptor del mismo. Interacción que actúa fundamentalmente por medio del dinamismo del destinatario.
Como consecuencia, desde la teoría del texto se considera la presencia de dos componentes que condicionan la transmisión del mensaje: las condiciones de producción y las condiciones de recepción. Las condiciones de recepción vienen dadas por una serie de características aportadas básicamente por el lector. Las condiciones de producción son las que propicia el emisor. Entre estas condiciones de producción, cuando se pretende conseguir una comunicación eficaz, se encontrarían las características básicas que recogen las fórmulas de predicción de lecturabilidad.
La constatación empírica, segunda de las líneas que se señalaban, viene dada por el hecho, cada vez más frecuente, de la aparición en el mercado de instrumentos informáticos para ayudar a los alumnos de distintos niveles de enseñanza en tareas de aprendizaje funcional del lenguaje, sobre todo por medio de la redacción. En este terreno, y sólo como ejemplo, cabe mencionar programas tales como Tools for Writers, de Thury (1986) o Grammatik Mac, de Reference Software International (1991).
El instrumento de Thury permite determinar las palabras poco precisas o ambiguas que aparecen en un determinado texto elaborado por los alumnos, hace recuentos de frecuencias, determina la amplitud del vocabulario utilizado por medio del cálculo de la tasa de redundancia, etc.
El Grammatic Mac incluye en el menú una valoración de la lecturabilidad basada en la fórmula de Flesh. Valora la lecturabilidad del texto construido por el alumno y le informa de su evaluación de modo inmediato. Esta valoración de la lecturabilidad, casi en tiempo real es una idea interesante, que podría aplicarse a la prensa, y sobre la que habrá que volver posteriormente.
2. LECTURABILIDAD Y LEGIBILIDAD
Podría ser oportuno iniciar el tema con unas precisiones terminológicas. Cabe esperar que después de una estipulación definicional, de un convenio sobre el sentido de ciertos términos, se incremente el nivel de comprensión de este texto. O al menos que se haga más unívoco.
Los términos lecturabilidad y legibilidad han sido utilizados como sinónimos en castellano. Uno y otro aludían a la facilidad o dificultad de un fragmento escrito para ser leído y entendido. Pero las jergas científicas surgen con la intención de matizar conceptos o territorios muy próximos. A este criterio responde la distinción que se realiza en inglés entre legibility y readability. Los equivalentes castellanos que cabría considerar serían precisamente los anteriormente aludidos: legibilidad y lecturabilidad.
Pero a nadie se le escapa la amplitud del concepto de lectura. Ya la caracterización clásica de Thorndike pone de manifiesto la presencia de, al menos,dos componentes en el acto lector:
«Leer no es sólo recrear la forma sonora de las palabras, sino también comprender» (Thorndike, 1921).
La recreación de la forma sonora de las palabras está exigiendo -supuestas las habilidades del sujeto lector- unas características formales en el texto que facilite la identificación de los grafemas. Esencialmente se trata de las características tipográficas del texto. Entendemos por legibilidad justamente esa facilitación tipográfica, tal como lo estudia, por ejemplo, Tinker (1963): tamaño, interlineación, justificación, subrayados, etc.
Pero la comprensión del sentido del texto supone toda una serie de procesos cognitivos que, evidentemente, pueden verse facilitados desde el exterior,mediante la utilización de diversos recursos que podríamos denominar, en sentido lato, estilísticos: complejidad de frases, utilización de vocablos usuales, etc. A esta perspectiva de facilitación de la comprensión, apoyada en las características del mensaje en sí y al margen de su presentación gráfica, llamaremos lecturabilidad. Como consecuencia cabría señalar que, en condiciones normales, un texto impreso es más legible que un manuscrito. Pero un cuento de Gloria Fuertes o de Andersen tiende a ser más lecturable que un fragmento de Hegel.
Uno de los campos más nítidamente definidos en la lingüística cuantitativa es el de la predicción de lecturabilidad, el del pronóstico de comprensión atribuible a un texto en tanto que puede ser leído por sujetos de determinadas características psicológicas o instructivas. La aplicación de estos modelos no queda sólo restringida al ámbito escolar por tanto. Todo aquel medio de comunicación que utilice textos escritos -prensa, revistas, folletos, programas, etc.- puede ser destinatario de estos estudios. Incluso se han efectuado acercamientos al mundo del lenguaje oral a partir de estas técnicas: la radio y la televisión también han sido usufructuarias a veces de estas predicciones.
Otra característica más de las fórmulas de lecturabilidad: no pueden importarse de un idioma a otro sin más. Ni siquiera son aceptables plenamente aquellas adaptaciones por analogía como las que efectúan por ejemplo Kandel y Moles con relación al francés (1958). Los estudios sobre lecturabilidad pueden replicarse, pero nunca traducirse.
3. LAS FORMULAS DE LECTURABILIDAD EN CASTELLANO
Las fórmulas de legibilidad clásicas, en castellano, han estado ligadas de forma habitual a la enseñanza. Sea con el objetivo de adaptar el material escrito -libros escolares sobre todo-para alcanzar una comunicación didáctica más eficaz, sea para estudiantes de español como segunda lengua. Tan sólo cabe señalar como fórmula que pretendía un cierto sentido de generalidad la de Patterson (1972), que intentaba facilitar un instrumento a predicadores religiosos a fin de promocionar material escrito más fácil para los hispanohablantes. Y hay que tener en cuenta que cabe, por extensión, considerar el trabajo para el que se creó como una forma de enseñanza…
Las fórmulas españolas se inician con Spaulding (1951, 1956), que propone, tras un proceso sucesivo de tanteos, la siguiente:
Dificultad lectora= 1,609 ASL – 331,8 D – 22
Fórmula en la que:
ASL= promedio de longitud de frases
D= densidad de vocabulario, evaluada a través de las palabras ausentes de la Density Word List de Spaulding, basada a su vez en el recuento de vocabulario castellano realizado por Buchanan (1941).
Poco después, Fernández Huerta (1959) basándose en la fórmula de Flesch (1948), determina el coeficiente de facilidad lectora de un texto a través de la fórmula:
Lecturabilidad= 206,84 – 0,60 P – 1,02 F
Donde:
P= número de sílabas por cada 100 palabras
F= número de frases por 100 palabras.
Los estudios de Alcobé (s.a.), dirigidos por Fernández Huerta en la Universidad de Barcelona continúan en esta línea.
Trabajos posteriores sobre el tema son los de Gutiérrez (1972), Patterson (1972), Thonis (1976), García (1977), Gillian, Peña y Mountain (1980), Vari-Cartier (1981) y Cradwford (1984, 1989).
Por nuestra parte, este tema se planteó en los años setenta en el Departamento de Didáctica de la Universidad de Valencia, donde se efectuó el primer trabajo de López Rodríguez (1976), que da lugar posteriormente a los de 1981 y 1982, dirigidos todos ellos por Rodríguez Diéguez.
Esta línea de trabajo se traslada posteriormente a la Universidad de Salamanca, en cuyo Departamento de Didáctica se efectúa una serie posterior de trabajos en esta misma línea (Rodríguez Diéguez, 1983, 1988, 1989).
Una interesante y sintética perspectiva de todos estos estudios aparece en el documentado estudio de Annette T. Rabin (1988).
Estos trabajos, en la Universidad de Salamanca, se cierran por ahora con los trabajos de Moro (1991), Cabero (1991) y Rodríguez Diéguez, Moro y Cabero (1992).
4.1. La descripción de las variables
Los estudios de lecturabilidad que hemos realizado, a través de diversos momentos, han ido considerando una amplia serie de variables que, sucesivamente, se han ido depurando. El número más amplio de variables predictoras utilizadas fue de 33, en el estudio de 1983. En el momento presente hemos reducido a doce las variables que utilizamos. A continuación se enumeran y presentan estas variables mediante la transformación que más frecuentemente se ha utilizado:
Variable 1. Pronombres
Total de pronombres que aparecen en el texto, expresado cuantitativamente mediante la siguiente fórmula:
(n pronombres 1 y 2 persona/n total de palabras del texto) X 1000
Variable 2. Vocabulario G-H
Usualidad del vocabulario, utilizando como referente el vocabulario usual de García Hoz (1953), convertido en indicador a partir de la siguiente transformación:
(palabras total del texto – palabras del diccionario/palabras total del texto) X 1000
Variable 3. Desviación típica
El valor de la desviación típica de la distribución de letras por palabra de cada uno de los textos.
Variable 4.Vocabulario TV
Usualidad del vocabulario del texto, evaluada con referencia al vocabulario usual obtenido por Lorenzo Delgado(1981) a partir de una muestra de programas de televisión, tratado a través de la misma fórmula que en la variable 2.
Variable 5. Palabras por frase
Proporción de palabras por frase en el total del texto que se evalúa.
(n pal. totales del texto/n de frases) X 1000
Variable 6. Total de puntos
Se expresaba mediante la fórmula:
(n puntos totales del texto/n palabras total del texto) X 1000
Variable 7. Total puntos y aparte
Se utilizó la fórmula:
(n total puntos y aparte/n total palabras texto) X 1000
Variable 8. Comas
Se calculó el indicador a partir de:
(n comas totales del texto/n palabras total texto) X 1000
Variable 9. Media más 2,58 sigmas
Se basa en la determinación de la media de letras por palabras en cada uno de los textos, a la que se le suma 2,58 veces el valor de la desviación típica de esa misma distribución. Más adelante realizaremos un análisis detenido de esta variable.
Variable 10. Puntos y coma
Este índice se calcula por medio de:
(n puntos y coma totales texto/n total palabras texto) X 1000
Variable 11. Nombres propios
Estimado a través del número de mayúsculas no justificadas ortográficamente que aparecen en el texto, y tratado con la fórmula:
(n mayúsculas- n total puntos/n total palabras texto) X 1000
Variable 12. Tasa de redundancia
modificada
El cálculo habitual del indicador TTR suele efectuarse directamente sobre el texto original. En este caso hemos considerado las formas lexemáticas, sin morfemas. La fórmula utilizada ha sido:
n pal. distintas del texto/n total palabras texto
Entre estas variables hay que distinguir tres grupos por sus características.
Un primer grupo está formado por aquellas que se basan en el simple recuento de frecuencias sobre el texto. Tales son el número de comas, de puntos y coma, de pronombres personales, etc.
El segundo está constituido por aquellas variables cuya fórmula, ya estandarizada, incluye de modo notorio el número de palabras totales del texto: tales son la tasa de redundancia, la desviación típica de la distribución de letras por palabra en cada texto, o el parámetro media más 2,58 sigmas.
Un tercer grupo es el de aquellas en las que, sin que haya esa alusión directa y clara al valor del total de palabras del texto, sin embargo la utilización tradicional en las fórmulas de lecturabilidad así lo ha efectuado. Los recuentos de vocabulario usual constituyen este tipo.
Las variables del primer grupo se vieron afectadas por el valor del número de palabras tal como aparecen en la descripción. Se tantearon otras vías alternativas de normalización de estos valores, siempre buscando la homogeneización con el número de palabras. En este caso se ha utilizado por primera vez la transformación arcoseno, que se expresa por la fórmula:
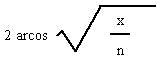
Donde x es el valor del recuento de incidencias de la variable en el total del texto, y n el total de palabras del texto que se valora. Esta fórmula demostró ser eficaz en el estudio que llevó a cabo Herrera (1982) sobre condiciones de producción de textos escritos por escolares de diversas edades, y se apoya en las propuestas de Dagnelie (1984) y Tejedor (1984).
Esta transformación se efectuó sobre las variables 1 (pronombres personales), 6 (total de puntos), 7 (puntos y aparte), 8 (comas), 10 (puntos y coma) y 11 (nombres propios).
Sin embargo, como ya se verá, fue necesario replantearse las transformaciones con relación a las variables 8 y 9.
4.2. El agrupamiento factorial de las variables independientes
Estas doce variables fueron valoradas en un conjunto de 200 fragmentos literarios cuyas características básicas eran la presencia cierre textual, la unidad de sentido claramente perceptible, y una extensión aproximada entre 250 y 500 palabras.
Las valoraciones de los doscientos textos en estas doce variables se sometieron a un análisis factorial de correlaciones. Se pretendía así facilitar las tareas de interpretación posterior de los datos, ya que el agrupamiento en factores simplifica la comprensión del conjunto de variables.
El análisis factorial proporcionó la siguiente matriz factorial rotada:
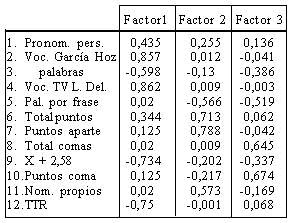
La estructura factorial es claramente invariante con las que hemos obtenido en otros momentos y con otras muestras (Beltrán de Tena, 1983, Rodríguez Diéguez, 1991).Los factores que la componen podrían describirse así:
4.2.1. El factor lexicográfico
El factor lexicográfico gira en torno a una serie de características de las palabras. Tasa de redundancia, número de pronombres, usualidad de vocabulario -tanto a partir del vocabulario de García Hoz como del de Lorenzo Delgado- y una variable peculiar: desviación típica de la distribución de letras por palabra y media más 2,58 sigmas. Será necesario extendernos en torno a esta última variable.
En cualquier fragmento escrito podemos establecer la distribución de frecuencias del número de letras por palabra, distribución que será obviamente distinta de fragmento a fragmento.
En esa distribución podemos calcular la media y la desviación típica. Y a partir de esos dos estadísticos se puede estimar la probabilidad de que aparezcan palabras de cierta longitud. Por ejemplo, el valor de la media de letras por palabra más/menos 2,58 sigmas marca el intervalo confidencial del 99 por ciento. El 99 por ciento de las palabras del texto cabe esperar que se encuentren en ese intervalo. Pero si se considera sólo una cola de la distribución, el nivel de confianza se incrementa al 99,5 por ciento. De este modo, tan solo cabe esperar que una palabra de cada doscientas tenga esa longitud. Se trata de una extrapolación de la longitud máxima esperable con esa probabilidad en ese texto concreto. Se podría decir que este indicador es una estimación de la máxima longitud esperable en las palabras utilizadas en un texto. Si un texto tiene como promedio de letras por palabra un valor de 9, y como desviación típica 1,03, el valor de 11,65 indicará la longitud máxima esperable tan solo en el 0,5 por ciento de palabras.
La longitud de palabra ha sido un indicador frecuentemente utilizado en las fórmulas de lecturabilidad en distintos idiomas, elaborado a partir de distintas valoraciones. La valoración de la longitud de las palabras es uno de los indicadores más clásicos en el ámbito de la lingüística cuantitativa. Y el indicador de longitud de palabras media más 2,58 sigmas, además de ser coherente, demuestra ser una estimación eficaz y más precisa que todas las efectuadas hasta ahora.
En las revisiones bibliográficas que hemos efectuado no hay referencia alguna a este indicador. Parece que su utilización no se ha producido en ninguna lengua. Es una aportación original de los estudios de Rodríguez Diéguez (1983, 1988, 1989, 1991, entre otros). Un estudio más completo de algunos aspectos de esta variable desde la perspectiva de las condiciones de producción puede verse en Herrera García (1992). Es necesario señalar que, con frecuencia, los valores de media más 2,58 sigmas y desviación típica tienen un valor predictivo similar, como se podrá ver por su presencia alternativa en algunas de las fórmulas.
Hay que añadir que este factor, pese a su carácter pretendidamente superficial, puede trascender esa perspectiva y convertirse en una explicación de carga cognitiva más profunda como ya se ha analizado (Rodríguez Diéguez, Moro y Cabero, 1992)
4.2.2. El factor fraseológico
El segundo factor definido en la estructura simple procedente del análisis factorial de las variables independientes podemos denominarlo factor fraseológico. Aparece definido por la conjunción de tres variables cuya concomitancia parece evidente: puntos y aparte, total de puntos, palabras por frase. Resulta menos explicable la presencia de la variable nombres propios.
La variable palabras por frase correlaciona en sentido contrario a las otras dos.
El análisis de este factor, desde nuestra perspectiva, debe hacerse en conjunción con el factor III, conceptualmente muy próximo a él. Esa proximidad viene marcada por la aparición de saturaciones exclusivamente asociadas a las variables relacionadas con los signos de puntuación en uno y otro caso.
Sin embargo, esa proximidad conceptual no se corresponde con una relación estadística. Inicialmente, la rotación es ortogonal, por tanto no existe intercorrelación entre los factores. Pero además, en un segundo análisis del conjunto de datos, se efectuó una rotación oblicua. Los factores se mantienen nítidamente. Y la correlación entre los factores II y III es tan sólo de 0,162.
4.2.3. El factor de dificultad sintáctica
Este tercer factor está constituido por las variables palabras por frase, puntos y coma y comas. La correlación entre la primera y las dos últimas aparece con sentido contrario.
Uno y otro factor responden a la estructuración del texto en frases. Pero el concepto de frase es suficientemente impreciso.
El problema queda en parte asociado a una dimensión de puntuación. Porque frases, párrafos, oraciones o sintagmas tienen un correlato relativamente estable con los signos de puntuación. Plano que no aparece suficientemente claro tampoco en esta otra perspectiva. La puntuación supone la presencia de una serie de signos. Y los signos de puntuación tienen una función específica: «encuadrar construcciones independientes, oraciones o estructuras insertas en la oración, proposiciones» (Salvador Mata, 1986).
El sentido relativamente nítido del punto y aparte se va progresivamente desdibujando al considerar el punto y seguido o el punto y coma. Se entra en una zona de matices cuyo correlato, frecuentemente estilístico, impide efectuar precisiones mayores. Pero desde nuestra perspectiva es conveniente señalar que la presencia de la variable punto y punto y aparte en un factor, frente a coma y punto y coma en el otro tiene que ver con esa nitidez que se alcanza a captar en la diferenciación progresiva entre los distintos signos de puntuación.
De aquí que la ruptura del texto en una serie de unidades de contenido suficientemente diferenciadas -caso del punto y seguido o el punto y aparte- se proyecte de un modo diferenciado con relación a la estructuración matizadamente presentada a través de los modos más delicados de presentar la información, tales como son las comas y los puntos y coma. La línea divisoria entre la diferenciación fuerte y la matizada puede encontrarse en la frontera entre el punto por una parte y el punto y coma por la otra.
5. LA VALORACIÓN DE LA COMPRENSIÓN DE LOS TEXTOS
La ecuación de predicción exige poner en relación los datos de las variables independientes o predictoras, variables que se obtienen directamente de los textos de los que se intenta predecir si serán fácil o difícilmente leídos, con datos de facilidad o dificultad lectora, obtenidos por algún criterio externo.
Los datos con los que hemos trabajado proceden de un estudio cuya finalidad -como en la casi totalidad de las fórmulas españolas- era la determinación de las ecuaciones de predicción para distintos niveles educativos. La pretensión actual es la de obtener, a partir de los datos anteriores, y mediante nuevos agrupamientos de los resultados, nuevas ecuaciones de predicción que nos den cuenta de cómo predecir en el supuesto de que la predicción se efectúe con resultados de buenos lectores o de lectores medios o con la muestra total.
Este planteamiento daría respuesta a las necesidades de lecturabilidad en revistas o periódicos cuyos destinatarios pudieran ser lectores identificables con el grupo general, con lectores bien capacitados, o con lectores medios.
El conjunto total de datos está constituido por una muestra de sujetos de nueve niveles educativos diferentes, y con 2000 sujetos por cada nivel.
Se trataba de que un total de diez sujetos de cada uno de los nueve niveles leyera cada uno de los doscientos textos que se habían seleccionado inicialmente. Y que respondiera a unas pruebas diferentes que pusieran de manifiesto cómo había entendido el fragmento literario que se le había proporcionado.
De este modo se trabajó con 2000 alumnos de cada uno de los siguientes niveles:
Educación General Básica: cuarto, sexto y octavo cursos.
Formación Profesional: Primero y Segundo Ciclos.
Bachillerato: Segundo Curso.
Curso de Orientación Universitaria.
Universitarios: segundo y cuarto curso de Filosofía y Ciencias de la Educación y Derecho.
La muestra se obtuvo en Salamanca.
Los estudios publicados a partir de estos datos han presentado los resultados para cada uno de los niveles educativos (Moro, 1991; Cabero, 1991; Rodríguez Diéguez, Moro y Cabero, 1992).
Sin embargo ahora pretendo, a partir de los datos anteriores, reagrupar las muestras de acuerdo con los criterios antes señalados, y obtener luego nuevas ecuaciones de predicción.
El nivel de buenos lectores estará formado por un total de 8000 alumnos que han leído 200 textos, y han respondido a las pruebas de comprensión, pertenecientes a los niveles educativos de segundo curso de Bachillerato, Curso de Orientación Universitaria y segundo y cuarto cursos de estudios universitarios.
Los lectores medios son diez mil sujetos de Educación General Básica y Formación Profesional.
La muestra total está constituida por la consideración de todos y cada uno de los niveles, textos y sujetos.
La comprensión lectora se evaluó, como ya se ha dicho, mediante la lectura de cada uno de los doscientos textos por parte de un grupo de diez alumnos de cada uno de los niveles educativos previstos. Cada uno de los alumnos respondió a las siguientes pruebas:
1. Una variante del test cloze, una de las pruebas más clásicas de comprensión lectora, y que ha sido frecuentemente utilizada, en otras lenguas, para la determinación de ecuaciones de predicción. Se utilizó una variante que se ha ido poniendo a punto progresivamente en el Departamento de Didáctica tras sucesivas tesis y tesinas. La técnica consiste en preparar un fragmento literario mediante la supresión de algunas palabras del texto. El producto resultante de esta supresión se presenta sustituyendo la palabra eliminada por unos espacios o líneas en blanco (Rodríguez Diéguez, 1991).
La valoración de resultados de la prueba cloze se efectuó de distintos modos, a fin de considerar si alguna de las variantes de recuento afectaba de modo sustantivo a los resultados. Estos modos fueron:
– Porcentaje total de aciertos sobre el número de espacios en blanco multiplicado por cien. Con esta primera forma de corrección se pretendía neutralizar la longitud del texto, ya que no todos tenían el mismo número de palabras.
– Otra vía de homogeneización de los resultados consistió en cortar todos los textos, a efectos de evaluación, para que tuvieran la misma longitud. Para ello se valoraron un total de 49 items cloze, número de elementos que aparecían en el texto más corto.
– La tercera puntuación asignada fue la puntuación directa del cloze, es decir el total de aciertos obtenidos por el sujeto en la prueba, independientemente de la longitud del texto.
– La puntuación directa del cloze menos las dos primeras líneas; con ello se pretendía conseguir un cierto entrenamiento de los sujetos que podría influir en el número de aciertos conseguidos.

2. Ideas principales del texto. Era la segunda prueba de comprensión, en la cual se pedía a los sujetos, una vez finalizada la realización de la prueba cloze, que escribiesen las tres ideas que considerasen principales de la lectura. Se valoraron de acuerdo con un análisis inicial de contenido de los textos.
El resultado de este proceso desembocaba en la atribución a cada uno de los textos de una serie de valoraciones cuantitativas proporcionadas por cada uno de los sujetos que las leyó. Y esa serie de puntuaciones, en cada uno de los textos y grupos globales se expresaban en su media. Los textos valorados por los denominados buenos lectores contarían, cada uno de ellos, con un total de cuarenta valoraciones de cada forma del cloze, y otras cuarenta de ideas, y los leídos por los lectores medios con cincuenta calificaciones, en función del número de subgrupos originarios que constituyen estos dos en los que ahora se agrupan.
3. Una tercera fuente de información se obtuvo mediante lo que se denominó calificación por jueces. Consistió en la lectura de los doscientos textos por diez jueces elegidos al azar. Estos tenían que asignar una puntuación a cada texto, que oscilaba entre cero y diez, en función de su dificultad o facilidad. Cuanto menor fuese la puntuación asignada a un texto mayor sería su dificultad y viceversa.
Esta serie de puntuaciones permiten contar con suficiente información cuantificada sobre la dificultad atribuible a cada uno de los doscientos textos.
El problema consistía ahora en el modo de combinar esa serie de calificaciones atribuidas a cada uno de los textos.
Para resolver este problema se procedió a analizar factorialmente los resultados de cada uno de los dos grandes grupos que se habían constituido ahora: Los resultados de cada una de las distintas pruebas cloze, de la valoración por jueces y de la valoración de ideas.
Los resultados de este análisis detectan la presencia de los dos factores siguientes:
Factor I o factor cloze, en el que se agrupan todas las variables relativas al test cloze. Inicialmente cabría identificarle con un factor superficial o formal, de corto calado cognitivo.
Factor II o factor ideas-jueces, donde se agrupan las variables de las ideas principales del texto y las valoraciones de los jueces. Es un factor que combina un determinado conocimiento lingüístico y una valoración global de su dificultad, ya que supone la expresión escrita de lo que se considera más importante, siendo destacable sobre todo en los cursos inferiores donde la producción escrita de los sujetos es bastante limitada. El juicio promedio de los jueces se asocia a la variable ideas.
El análisis factorial proporciona -como ya se vio en el primero de los presentados- una simplificación del conjunto de variables, expresadas en un conjunto de constructos más corto en número que son los factores. Los factores son el agrupamiento de variables que tienen algo en común. Y a los sujetos, valorados en todas esas variables, se les puede valorar también, de modo más sintético, en los factores en los que las variables se agrupan. Son las puntuaciones factoriales. Y fueron las puntuaciones factoriales las que se utilizaron como variables criterio.
6. LAS PECULIARIDADES DE ESTE ESTUDIO
Como consecuencia, en este estudio pretendemos realizar unas predicciones que presentan como características peculiares las siguientes:
– Un reagrupamiento de las muestras, a fin de que permitan considerar ahora las situaciones generales, no definidas en función estricta de los niveles educativos. La presencia de tales niveles en la determinación inicial de las cuotas de participación de cada subconjunto permiten, sin grave licencia, aceptar que una muestra de lectores podría adscribirse a la muestra de lectores medios, que ha considerado un total de 10.000 evaluaciones, la muestra total de lectores, de 18.000 sujetos, y la muestra de buenos lectores, constituida por 8.000 valoraciones.
– La valoración de algunas de las variables predictoras mediante la transformación arcoseno.
– La integración en el criterio de valoración de puntuaciones de tres procedencias -cloze, ideas y jueces- y tratadas en todos los casos mediante la consideración de los dos factores primeros obtenidos en el análisis factorial del conjunto de variables criterio.
7. LA ECUACIÓN DE PREDICCIÓN GLOBAL
A partir de estos datos, se va a presentar, como conclusión de este artículo, la ecuación de predicción del grupo total, con base en las 18.000 valoraciones efectuadas.
La predicción sobre las puntuaciones factoriales del primer factor alcanzó una correlación múltiple de 0,678
La ecuación de predicción es la siguiente:
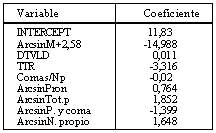
La predicción del segundo factor alcanza una correlación de 0,33. La ecuación queda definida por las cuatro variables siguientes:
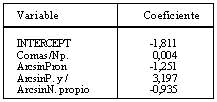
La ecuación de predicción para buenos lectores
Considerábamos buenos lectores a efectos de predicción a los sujetos procedentes de la muestra de Bachillerato, C.O.U. y estudios universitarios. Estaba formada esta muestra por un total de 8.000 alumnos que han leído los 200 textos, y han respondido a las pruebas de comprensión, pertenecientes a los niveles educativos de segundo curso de Bachillerato, Curso de Orientación Universitaria y cursos segundo y cuarto de estudios de Derecho y Filosofía y Ciencias de la Educación.
A partir de esta muestra, la ecuación de predicción para el factor I alcanza una correlación múltiple de 0,656, y es la siguiente:
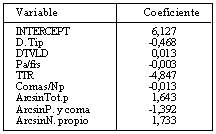
Para el factor II, con una correlación múltiple de 0,336, la ecuación se define así:

8. LA ECUACIÓN DE PREDICCIÓN PARA LECTORES MEDIOS
Considerábamos lectores medios a aquellos sujetos que serían asimilables a los niveles iniciales de enseñanza que habíamos estudiado. Los lectores medios estarían representados por las diez mil valoraciones de textos realizadas a partir de sujetos de Educación General Básica y Formación Profesional.
En el factor I se consigue una correlación de 0,666 con la siguiente combinación de variables en la ecuación:
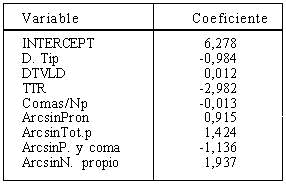
En el factor II la correlación es 0,347, y las variables y coeficientes son los siguientes:
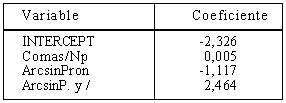
Llama la atención de entrada la presencia en las ecuaciones del primer factor, en los tres casos, de las mismas variables: salvo palabras por frase que sustituye en la ecuación de buenos lectores a la variable pronombres, y X+2,58 que sustituye a desviación típica en los lectores medios, los componentes son los mismos: desviación típica de las palabras del texto, usualidad evaluada a través del vocabulario de Lorenzo Delgado, tasa de redundancia, comas, total de puntos en el texto, puntos y coma y nombres propios. Hay que recordar la precisión que ya se hizo en el anterior artículo con relación a las variables desviación típica y X+2,58 en lo relativo a su solapamiento.
Estas variables se reparten por los tres factores del análisis factorial inicial, si bien es el primero, el factor lexicográfico, el que aporta mayor número de variables.
Esta asociación permite intuir que la evaluación de la comprensión a partir de la prueba cloze es, frente a la suposición inicial y frecuente, algo más que una pura prueba de memoria. Y justamente la toma de conciencia de esta superación de una valoración mecanicista es lo que ha extendido notablemente su uso como prueba de comprensión.
Este primer factor es, en todos los casos, el que alcanza una valoración más alta en su predicción. La correlación oscila entre 0,656 y 0,680, explicando una varianza de un 43 a un 46 por ciento, y una varianza ajustada en todos los casos superior al 40 por ciento.
Todas las variables superan el valor de probabilidad del 5 por ciento, excepto palabras por frase en la ecuación de buenos lectores (14 por ciento, pero con un valor de F suficiente), y puntos y coma en la ecuación de lectores medios (8 por ciento, y valor de F suficiente a un nivel del 5 por ciento).
Es también interesante constatar que en todos los casos, en el proceso de inclusión de variables a través del método stepwise la variable comas se ha introducido a través de la transformación que supone dividir el número de comas por el total de palabras en lugar de mediante la transformación arcoseno, que ha predominado en las restantes variables.
La predicción del factor II en los tres casos alcanza un valor más reducido. Los coeficientes de correlación se mueven en una banda de valores de 0,33 a 0,347, con una proporción de varianza explicada del 10 al 12 por ciento, que se reduce entre 9 y 11 por ciento en los valores ajustados.
Las variables permanecen con una relativa constancia en las ecuaciones de predicción de lectores medios y en la predicción global: comas, pronombres, puntos y aparte. En la muestra de buenos lectores se produce un cambio de relativa importancia: el componente fraseológico aparece también, pero en este caso por medio de la variable total puntos.
El factor fraseológico es el que mayor número de variables aporta a esta fórmula, y se constata la presencia de una relativa invarianza, menos fuerte que en el factor I. Los buenos lectores, sin embargo, presentan en la ecuación de predicción componentes del factor I: TTR y desviación típica.
10. LA UTILIZACIÓN DE LAS FÓRMULAS
El sentido último de las fórmulas de lecturabilidad es la de ser utilizadas para facilitar las condiciones de recepción del mensaje verbal a partir de las condiciones de producción.
Las fórmulas, en sus orígenes, exigían un esfuerzo notable para ser aplicadas y mejorar la comprensión de un texto a partir de los indicadores suministrados. El problema no era otro que el del tiempo, que es el eje del trabajo en la redacción del periódico. Redactar un artículo, evaluar las variables de modo más o menos manual, aplicar las fórmulas, y recomendar al escritor que vuelva a escribirlo teniendo en cuenta que no debe utilizar palabras tan largas, que debe incluir mayor número de puntos y menor de comas resultaba a todas luces imposible de llevar a cabo en la redacción de un diario.
Sin embargo las condiciones de trabajo han modificado notablemente su posible uso. Una fórmula de lecturabilidad puede ir siendo calculada al tiempo que el escritor va elaborando su texto sobre la pantalla. El cálculo parcial del coeficiente en determinados momentos es posible y fácil a través de programas que podrían asociarse al tratamiento de textos utilizado en cada medio. La indicación al autor puede hacerse así en tiempo real. La valoración didáctica que hacen Grammatic Mac o Tools for Writers puede realizarse también como final de un artículo o en los momentos en los que el autor estime oportuno efectuarlo.
El recuento de letras por palabra, la comparación con diccionarios y, como final, la sugerencia de las modificaciones a realizar en el texto son un problema rutinario si se cuenta con las ecuaciones que formalizan la predicción.
11. UN EJEMPLO DE APLICACIÓN DEL PROCESO
Voy a presentar un ejemplo elaborado a partir del uso didáctico de las fórmulas.
Supongamos que solicitamos a dos autores, para un libro de texto de Bachillerato, una breve versión de la fábula de Esopo Los ratones y el gato.
Imaginemos que se pretende conseguir una formulación eficaz en su lectura, un texto que resulte de fácil lectura para los alumnos.
Una de las ecuaciones de predicción aplicables a Bachilllerato, con criterio basado en un único factor, y que se podría utilizar en este caso es la siguiente:
Indice de dificultad = 3,416 – 0,892 s
– 4,336 TTR + 0,099 VGH – 0,322 Comas
– 1.059 Puntos y coma.
Las versiones que nos proporcionan los autores a los que se les solicitan los textos son las siguientes:
Versión a/
«Hace ya mucho tiempo, los ratones celebraron una asamblea general con el fin de considerar qué medidas podrían adoptar para librarse del enemigo común: el gato. Después de discutir varios proyectos, sin resultado alguno, se levantó un ratón joven y declaró que tenía que hacer una proposición que no dudaba que sería la más acertada.
– Convendréis conmigo -dijo- que el peligro principal que corremos es la silenciosa y taimada aproximación del enemigo. En cambio, si nos revelase su presencia por medio de alguna señal, escaparíamos de sus uñas sin esfuerzo. Propongo, pues, que se busque un cascabel y que se ate, con una cinta, al cuello del gato. Así sabremos cuándo llega y podremos escondernos hasta que se haya marchado.
La proposición fue acogida con una salva de aplausos. Entonces se levantó un ratón viejo y habló:
– Todo esto está muy bien -dijo, pero ¿quién le pondrá el cascabel al gato?
Los ratones se miraron unos a otros y nadie replicó una palabra. Entonces el viejo ratón sentenció:
– No hay nada más fácil que proponer remedios imposibles.»
El otro autor al que se le solicitó la redacción pensó que la forma rimada sería más adecuada, y presentó la siguiente versión.
Versión b/
Juntáronse los ratones
para librarse del gato;
y después de largo rato
de disputas y opiniones
dijeron que acertarían
en ponerle un cascabel
que andando el gato con él
librarse mejor podrían.
Salió un ratón barbicano
colilargo, hociquirromo,
y encrespando el grueso lomo
dijo al senado romano
después de hablar culto un rato:
– ¿Quién de todos ha de ser
el que se atreva a poner
ese cascabel al gato?
Aplicando la fórmula presentada para alumnos de Bachillerato, la versión a/ nos arrojaría un valor de predicción de
– 0,3676
El valor de predicción se presenta en este caso en una escala cuya media es cero, y que los valores negativos señalan ciertas dificultades de interpretación previsibles, frente a los positivos que indican tendencia a la facilidad en la lectura. Un texto con 3 puntos positivos sería un texto de facilísima lectura. Un coeficiente de -3 se atribuiría a un texto de muy difícil comprensión.
La versión a/ se situaría en una zona de relativa normalidad, si bien con ligera tendencia a la dificultad lectora. El pronóstico de lecturabilidad que podría hacerse de esta versión a/ sería:
Texto adecuado a alumnos de Bachillerato, con un nivel de dificultad ligeramente superior a la media.
La versión b/, por su parte, aparecería valorada, mediante la aplicación de la fórmula con un coeficiente de lecturabilidad de
-1,237
El pronóstico en este caso sería:
Este texto presenta un nivel alto de dificultad para estudiantes de Bachillerato.
Hay que tener en cuenta que su corta longitud y el conocimiento generalizado del tema son datos que contribuyen a la suavización de esta dificultad.
Hasta aquí nada nuevo nos han dicho las fórmulas. La valoración aproximativa de la lecturabilidad podría haberla realizado sin mayores dificultades cualquier lector medianamente experimentado. Sin embargo su mayor virtualidad radica en el posible análisis posterior de las variables, así como la búsqueda de normas que contribuyan a incrementar la eficacia comunicativa del texto.
Si comparamos el valor que obtiene cada una de las variables de la ecuación en cada una de las versiones con las valoraciones obtenidas en una muestra de textos, los datos son más expresivos y podrían ser más adecuados. La versión a/ tiene los siguientes valores en las variables implicadas en la ecuación:
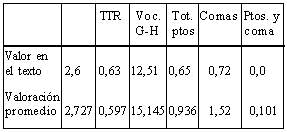
De acuerdo con estos datos, los indicadores que favorecen la lectura en la versión a/ de este texto son el número de comas, que es corto y la ausencia de puntos y coma.
Resulta neutral en cuanto a su incidencia en la lectura el tipo de vocabulario, que aparece, facilitado por el parámetro , y dificultado por el indicador de usualidad. De todos modos, la utilización de un vocabulario más adecuado, más corriente, más usual, facilitaría la lectura del texto.
Dificultan la lectura del texto la tasa de redundancia (TTR) y el corto número de puntos y seguido y puntos y aparte.
Para la versión b/, los valores de las variables consideradas de acuerdo con la ecuación de predicción son:
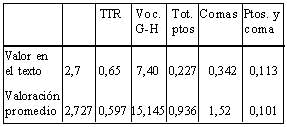
La única variable favorecedora en este texto es el número de comas utilizadas.
Las variables que dificultan la lectura, por el contrario, son el alto número de palabras no usuales que aparecen, el corto número de puntos y la baja tasa de redundancia.
Si resultara de interés incrementar la lecturabilidad de este fragmento, habría que pedir a su autor que:
a/ Eliminara palabras no usuales del texto. Esta es la característica más notoria de términos tales como barbicano, colilargo, hociquirromo, encrespar y otras similares.
b/ Utilizara un mayor número de puntos.
c/ Incrementara la tasa de redundancia.
Si D. Félix Lope de Vega y Carpio, autor de esta segunda versión, accediera a esta petición, en aplicación de los criterios de lecturabilidad, y modificara así el texto, la facilidad de comprensión del texto se incrementaría. El único problema sería que se podría perder para la posteridad una versión tan deliciosa de la fábula de los ratones y el cascabel.
12. CONCLUSIÓN
Análisis de este tipo, efectuados a partir de la redacción que se va efectuando al teclado, pueden ir sugiriendo al autor vías para facilitar las condiciones de lectura del texto. El proceso, en la actual situación de la redacción de los periódicos es de notable facilidad.
Siempre sería necesario tener en cuenta que la fórmula de lecturabilidad no es otra cosa que una simple orientación y que en modo alguno una valoración alta en el índice de facilidad lectora garantiza la interpretación del texto por parte de lectores hipotéticamente coincidentes con aquellos de los que se obtuvo la fórmula.
De las limitaciones de las fórmulas de lecturabilidad habla suficientemente el siguiente hecho: podemos generar textos cuya ecuación de lecturabilidad sea muy alta, y que, pese a ello, resulte absolutamente incomprensible. Bastaría con enumerar una serie de palabras usuales, de longitud similar, separadas por puntos cada tres o cuatro palabras, y sin comas. La predicción sería muy alta.
«Resulta respuesta rara. Pintor poeta también policía. Resulta respuesta rara. Pero cuida esta culpa.Resulta respuesta rara.Pintor poeta también policía.»
Este texto alcanzaría valores cercanos a 2,5 ó 3. Las palabras tienen una longitud que oscila entre cuatro y siete letras. Todas ellas son usuales de acuerdo con el criterio utilizado. No hay comas y sí frecuentes puntos. La repetición de las frases garantiza un valor alto de la tasa de redundancia. Pero no tiene sentido.
Es evidente que su comprensión no es fácil. Sobre todas las exigencias formales de las ecuaciones de predicción juega un papel definitivo la coherencia del texto que se examina.
La ecuación de predicción de lecturabilidad se convierte así en una ayuda inestimable para valorar y reescribir un texto con la intención de incrementar la eficacia comunicativa por la vía de facilitar las condiciones de producción del mismo. Pero es evidente que no es más que una ayuda.
Alcobe, A. (s.a.): Comprensión lectora en niños y niñas. Memoria de Licenciatura, inédita. Universidad de Barcelona.
Beltrán de Tena, R. (1983): «El proceso de comprensión lectora. Resultados de una investigación», en El Sistema Educativo Hoy. Proyecto Cinae, Buenos Aires, págs. 403-414.
Buchanan, M.A. (1941): A Graded Spanish Word Book. Univ. de Toronto Press, Toronto.
Cabero Pérez, M.V. (1991): Fórmulas de Legibilidad en Lengua Castellana para los Niveles Educativos de B.U.P. y Enseñanza universitaria. Tesis doctoral, inédita. Departamento de Didáctica, Universidad de Salamanca.
Cradwford, A.N. (1984): «A Spanish Language Fry-tipe Readability Procedure». Elementary Level Bilingual Education Paper Series. Evaluation, Dissemination and Assesment Center, California State University, Los Angeles.
Crawford, A.R. (1989): «La comprensibilidad de textos en español del nivel primario. Fórmula y gráfico, en AA.VV.: Leer en la escuela, Fundación G.S.R. y Ed. Pirámide, Madrid, págs. 274-283.
Dagnelie, P. (1984). Théorie et méthodes statisques. Les Presses agronomiques de Gembloux, Gembloux (Bélgica).
Fernández Huerta, J. (1959): «Medidas Sencillas de Lecturabilidad», Consigna, núm. 214, págs. 29-32.
Flesch, R.E. (1948): The Art of Readable Writing. Harper & Brothers, Nueva York.
García, W.F. (1977): «Assesing Readability for Spanish as a Second Language: The Fry Graph And Cloze Procedure». Dissertation Abstract, 38, 136a.
García Hoz, V.(1953): Vocabulario usual, vocabulario común y vocabulario fundamental. Determinación y análisis de sus factores. CSIC, Madrid.
Gillian, B; Peña, S.C.; y Mountain, L. (1980): «The Fry Graph Applied to Spanish Readability». The Reading Teacher, 3, 19426-430.
Gutiérrez de Polini, L.E. (1972): Investigación sobre lectura en Venezuela. Documento presentado a las Primeras Jornadas de Educación Primaria. Ministerio de Educación, Caracas.
Herrera García, E. (1992): Evolución del lenguaje escrito en los niños. Tesis doctoral inédita. Universidad de Salamanca.
Kandel, L. y Moles, A.A. (1958): «Application de l’Indice de Flesch a la Langue Française», en Cahiers d’Etudes de Radio Television, núm. 9, págs. 252-275.
López Rodríguez, N. (1976): Indicadores cuantitativos de comprensión lectora en textos narrativos. Memoria de Licenciatura. Departamento de Didáctica de la Universidad de Valencia (inédita).
López Rodríguez, N. (1981): Fórmulas de Legibilidad Para la Lengua Castellana. Tesis Doctoral. Departamento de Didáctica,, Universidad de Valencia.
López Rodríguez, N. (1982): Cómo valorar textos escolares. Ed. Cincel, Madrid.
Lorenzo Delgado, M. (1981): El vocabulario televisivo y su inserción en la enseñanza. I.C.E. Universidad de Granada.
Moro Berihuete, P. (1991): Fórmulas de lecturabilidad en lengua castellana para los niveles educativos de EGB y FP. Tesis Doctoral, Inédita. Departamento de Didáctica, Universidad de Salamanca.
Patterson, F.W (1972): Cómo escribir para ser entendido. Casa Bautista de Publicaciones, El Paso.
Rabin, A.T. (1988): «Determining Difficulty Levels of Text Written in Languages other than English», en Zakaluck, B.l. y Samuels, S.j. (ed): Readability. Its Past, Present & Futur. Ira, Newark, Delaware, págs. 46-76.
Reference Sofware International (1990): Grammatic Mac. The Easiet Way to Improve your Writing. San Francisco, California.
Rodríguez Diéguez, J.L. (1983): «Evaluación de textos escolares», Revista de Investigacion Educativa, vol. I, núm. 2, págs. 259-279.
Rodríguez Diéguez, J.L. (1988): «La lecturabilidad del material escrito», en Cuestiones de Didáctica. Homenaje a J. Fernández Huerta, de J.L. Rodríguez Diéguez (ed.). Sociedad Española de Pedagogía. CEAC, Barcelona págs. 219-230.
Rodríguez Diéguez, J.L. (1989): «Predicción de la lecturabilidad de textos en castellano: Una propuesta y algunas sugerencias», en Leer en la Escuela. Nuevas Tendencias en la Enseñanza de la Lectura, págs. 284-310, Ed. Pirámide/Fundación Germán Sánchez Ruipérez, Madrid.
Rodríguez Diéguez, J.L. (1991): «Evaluación de la comprensión lectora», en A. Puente (ed.): Comprensión de la lectura y acción docente. Fundación Germán Sánchez Ruipérez y Ed. Pirámide. Madrid, págs. 301-345.
Rodríguez Diéguez, J.L., Moro Berihuete, P. y Cabero Pérez, M. (1992): La predicción de la lecturabilidad de los textos escritos. Comunicación presentada en el X Congreso Nacional de Pedagogía, Salamanca.
Salvador Mata, F. (1986): «Aspectos didácticos del texto escrito por los alumnos del Ciclo Medio de E.G.B. Estudio evolutivo y diferencial». Rev. Española de Pedagogía, 171, págs. 97-115.
Spaulding, S. (1951): «Two Formulas for Estimating the Reading Difficulty of Spanish», en Educational Research Bulletin, núm. 30, págs. 117-124
Spaulding, S. (1956): «A Spanish Readability Formula», en Modern Language Journal, núm. 40, págs. 433-441.
Tejedor, F.J. (1984): Análisis de varianza aplicado a la investigación en Pedagogía y Psicología. Ed. Anaya, Madrid.
Thonis, E.W. (1976): Literacy for America’s Spanish Speaking Children. International Reading Association, Newark.
Thorndike, E.L (1921): The Teacher’s Word Book. Teacher’s College, Columbia Univ., Nueva York.
Thury, E.M. (1986): Tools for Writers. Apple Computer Inc., Cupertino, California.
Tinker, M.A. (1963): Legibility of Print. Iowa State University Press, Ames, Iowa.
Vari-Cartier, P: (1981): «Development and Validation of a New Instrument to Asses the Readability of Spanish Prose». Modern Langage Journal, 65, págs. 141-148.
Artículo extraído del nº 37 de la revista en papel Telos



Comentarios